progintro @ dit

Στόχος της εργασίας είναι να γράψουμε μερικά ακόμα προγράμματα σε C με χρήση βασικών τύπων και συναρτήσεων. Συγκεκριμένα, στοχεύουμε σε εμπειρία με τα ακόλουθα:
-
Χρήση ορισμάτων από την γραμμή εντολών
-
Χρήση συναρτήσεων
-
Χρήση αναδρομής
-
Χρήση δομών επανάληψης με διαφορετικά κριτήρια τερματισμού
-
Χρήση αλγοριθμικών απλοποιήσεων
Υποβολή Εργασίας.
Όλες οι υποβολές των εργασιών θα γίνουν μέσω GitHub και συγκεκριμένα στο github.com/progintro (‘Οργανισμός για το μάθημα (GitHub progintro) ’, χ.χ.). Προκειμένου να ξεκινήσεις, μπορείς να δεχτείς την άσκηση με αυτήν την: πρόσκληση (‘Πρόσκληση για Εργασία 1 ’, χ.χ.).
Ο Αλγόριθμος του Ευκλείδη (gcd - 50 Μονάδες)
Ο Ευκλείδης (‘Euclid’, χ.χ.) ήταν πολύ τυχερός. Μεγάλωσε το 300 π.Χ. στην Αλεξάνδρεια (‘Alexandria’, χ.χ.), το πολιτισμικό κέντρο της Μεσογείουγια κάποιους το λίκνο του μοντέρνου κόσμου (Pollard και Reid 2006)και έχει άμεση πρόσβαση στην … Wikipedia της εποχής (‘Library of Alexandria’, χ.χ.). Ο κόσμος γύρω του αλλάζει γρήγορα, η φιλοσοφία και τα μαθηματικά ανθούν και ο ίδιος δεν κάθεται με σταυρωμένα χέρια. Συγκεντρώνει όλα τα γνωστά μέχρι τότε μαθηματικά και συνθέτει τα “Στοιχεία”, μια πραγματεία 13(!) τόμων η οποία 23 αιώνες αργότερα θα θεωρηθεί από τα σημαντικότερα κείμενα που έχουν γραφεί (‘Euclid’s Elements’, χ.χ.). Στις προτάσεις 1-2 του 7ου τόμου, ο Ευκλείδης περιγράφει έναν αλγόριθμοη λέξη αλγόριθμος δεν θα εφευρεθεί για 1000+ ακόμα χρόνια (‘Algorithm comes from Al-Khwarizmi’, χ.χ.)ο οποίος χρησιμοποιείται ακόμα και σήμερα. Προς τιμήν του, ο αλγόριθμος αυτός λέγεται Αλγόριθμος του Ευκλείδη (‘Euclidean Algorithm’, χ.χ.).
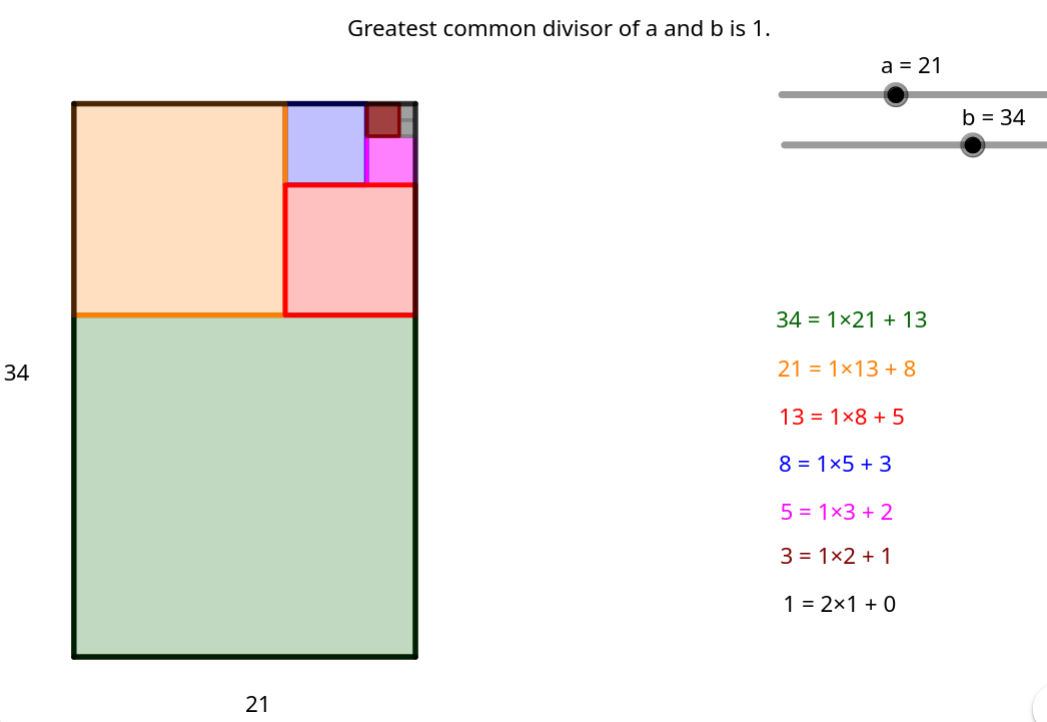
Γεωμετρική οπτικοποίηση (‘Euclid Algorithm Visualization’, χ.χ.) του υπολογισμού που πραγματοποιεί ο αλγόριθμος του Ευκλείδη για την εύρεση του μέγιστου κοινού διαιρέτη. Σε κάθε επανάληψη, υπολογίζουμε πόσες φορές χωράει η μικρότερη πλευρά στην μεγαλύτερη και συνεχίζουμε με το υπόλοιπο μέχρι το μέγεθος της μιας πλευράς να διαιρεί την άλλη. </figcaption> </figure>
Ο αλγόριθμος του Ευκλείδη (Euclidean Algorithm) μας βοηθάει να λύσουμε το πρόβλημα του Μέγιστου Κοινού Διαιρέτη (ΜΚΔ) ή Greatest Common Divisor (GCD) στα Αγγλικά. Αν σας θυμίζει κάτι, έχετε καλή μνήμη· το πρόβλημα του ΜΚΔ το είχαμε ξαναδεί στο Δημοτικό! Τότε το λέγαμε “μου-κου-δου”, αλλά επειδή οι περισσότεροι μάλλον το απωθήσαμε από την μνήμη μας (για προφανείς λόγους) προσφέρουμε εδώ μια υπενθύμιση: δοθέντων δύο αριθμών $a$ και $b$ ο μέγιστος κοινός διαιρέτης τους είναι ο μέγιστος αριθμός $d$ ο οποίος διαιρεί τους $a$ και $b$ χωρίς να αφήνει υπόλοιπο. Η έκφραση “διαιρεί χωρίς να αφήνει υπόλοιπο” είναι τόσο κοινή που συχνά απλοποιείται σε “διαιρεί”. Πιο επίσημα, έχουμε τους ορισμούς:
Ορισμός 1. Αν ο $a$ και ο $b$ είναι ακέραιοι με $a\neq 0$, λέμε ότι *ο $a$ διαιρεί τον $b$ αν υπάρχει ακέραιος $c$ έτσι ώστε $b = a \cdot c$. Όταν ο $a$ διαιρεί τον $b$ λέμε ότι ο $a$ είναι παράγοντας του $b$ και ότι ο $b$ είναι πολλαπλάσιο του $a$. Ο συμβολισμός $a \mid b$ σημαίνει ότι ο $a$ διαιρεί τον $b$ ($b\bmod a = 0)$. Αντίθετα $a \nmid b$ συμβολίζει ότι ο $a$ δεν διαιρεί τον $b$ ($b\bmod a \neq 0$).*
Ορισμός 2. Έστω ότι οι $a$ και $b$ είναι ακέραιοι, όχι μηδενικοί και οι δύο. Ο μεγαλύτερος ακέραιος $d$ έτσι ώστε να είναι $d\mid a$ και $d \mid b$ ονομάζεται *μέγιστος κοινός διαιρέτης των $a$ και $b$ και συμβολίζεται με $gcd(a, b)$.*
Για να δούμε πως μπορούμε να λύσουμε ένα τέτοιο πρόβλημα. Έστω ότι οι δύο ακέραιοι είναι: το $42$ και το $18$. Στο Δημοτικό, προκειμένου βρούμε το ΜΚΔ παραγοντοποιούσαμε τους δύο αριθμούς και ο ΜΚΔ ήταν ήταν το γινόμενο των κοινών παραγόντων. Η παραγοντοποίηση του $18$ είναι: $2 \cdot 3^2$ ενώ του $42$ είναι $2 \cdot 3 \cdot 7$ και επομένως οι $2\cdot 3$ είναι κοινοί παράγοντες και $gcd(42, 18) = 6$.
Η παραγοντοποίηση δεν είναι κακή μέθοδος αλλά είναι γενικά δύσκολη (‘Factorization’, χ.χ.). Ο αλγόριθμος του Ευκλείδη προτείνει κάτι σχετικά πιο εύκολο1:
\[\begin{aligned} \label{eq:gcd} \text{gcd}(a, b) = \begin{cases} b & , \text{if } a\bmod b = 0 \\ \text{gcd}(b, a \bmod b) & , \text{otherwise} \end{cases} \end{aligned}\]Για να “τρέξουμε” την αναδρομική Εξίσωση [eq:gcd] για το παράδειγμά μας: $\text{gcd}(42, 18)$. Έχουμε ότι $42\bmod 18 = 6$ (διάφορο του 0) και επομένως παίρνουμε τον δεύτερο κλάδο της συνάρτησης και υπολογίζουμε το $\text{gcd}(18, 42 \bmod 18) = \text{gcd}(18, 6)$. Τώρα όμως έχουμε ότι $18 \bmod 6 = 0$ και επομένως από τον πρώτο κλάδο της συνάρτησης έχουμε: $\text{gcd}(18, 6) = 6$. Συνεπώς πήραμε και πάλι το αναμενόμενο αποτέλεσμα: $\text{gcd}(42, 18) = 6$. Εύκολο; Θα δείξει!
Για το ζητούμενο αυτής της άσκησης λοιπόν, καλείστε να γράψετε ένα πρόγραμμα $gcd$ που υπολογίζει αυτόματα και αποδοτικά τον μέγιστο κοινό διαιρέτη δύο ακεραίων αριθμών χρησιμοποιώντας τον αναδρομικό αλγόριθμο του Ευκλείδη.
Τεχνικές Προδιαγραφές
-
Repository Name: progintro/hw1-<YourUsername>
-
C Filepath: gcd/src/gcd.c
-
Το πρόγραμμά θα πρέπει να παίρνει δύο ακεραίους αριθμούς στο δεκαδικό σύστημα ως ορίσματα από την γραμμή εντολών στην μορφή
./gcd num0 num1. Αν το πρόγραμμα εκτελεστεί με ορίσματα που δεν ακολουθούν τις παραπάνω προδιαγραφές, πρέπει να εκτυπώσει αντίστοιχο μήνυμα όπως στα παρακάτω παραδείγματα και να επιστρέφει με κωδικό εξόδου (exit code) 1. -
Όλες οι παράμετροι θα είναι στο εύρος $[-10^{18}, 10^{18}]$. Σε περίπτωση που δοθεί το μηδέν (0) το πρόγραμμά σας πρέπει να επιστρέφει με κωδικό εξόδου 1.
-
Το αρχείο C που θα υποβληθεί πρέπει να μεταγλωττίζεται χωρίς ειδοποιήσεις για λάθη και με κωδικό επιστροφής (exit code) που να είναι 0. Συγκεκριμένα, το αρχείο σας πρέπει να μπορεί να μεταγλωττιστεί επιτυχώς με την ακόλουθη εντολή σε ένα από τα μηχανήματα του εργαστηρίου (linuxXY.di.uoa.gr):
gcc -O3 -Wall -Wextra -Werror -pedantic -o gcd gcd.c -
README Filepath: gcd/README.md
-
Ένα αρχείο που να περιέχει στοιχεία εισόδου και ένα εξόδου διαφορετικά από αυτά της εκφώνησης. Συγκεκριμένα προτείνουμε να βάλετε έναν συνδυασμό που θεωρείται ότι είναι δύσκολος να γίνει σωστός.
-
input Filepath:
gcd/test/input.txt -
output Filepath:
gcd/test/output.txt
Παράδειγμα που όμως δεν θα γίνει δεκτό από την άσκηση επειδή είναι ήδη στα παραδείγματα παρακάτω, για το input.txt: “
942 1042” και για το output.txt: “2”. -
-
Πρέπει να ολοκληρώνει την εκτέλεση μέσα σε: 1 δευτερόλεπτο.
Παρακάτω παραθέτουμε την αλληλεπίδραση με μια ενδεικτική λύση:
$ hostname
linux14
$ gcc -O3 -Wall -Wextra -Werror -pedantic -o gcd gcd.c
$ ./gcd
Usage: ./gcd <num1> <num2>
$ echo $?
1
$ ./gcd 1
Usage: ./gcd <num1> <num2>
$ ./gcd 18 42
gcd(18, 42) = 6
$ ./gcd 42 18
gcd(42, 18) = 6
$ ./gcd -42 18
gcd(-42, 18) = 6
$ ./gcd 982451653 776531401
gcd(982451653, 776531401) = 1
$ ./gcd 78423360000000000 35241600000000000
gcd(78423360000000000, 35241600000000000) = 960000000000
$ ./gcd 68719476736 84767329979727872
gcd(68719476736, 84767329979727872) = 68719476736
$ echo $?
0
$ time ./gcd 1000000000000000000 999999999999999999
gcd(1000000000000000000, 999999999999999999) = 1
real 0m0.009s
user 0m0.004s
sys 0m0.004s0
nan
Στο αρχείο README.md πρέπει να προσθέσετε οποιεσδήποτε παρατηρήσεις σας κατά την διεκπεραίωση της άσκησης. Ο κώδικας απαιτείται να είναι καλά τεκμηριωμένος με σχόλια καθώς αυτό θα είναι μέρος της βαθμολόγησης.
Ο Αλγόριθμος RSA (rsa - 50 Μονάδες)
Κάθε φορά που συνδέεστε στο εργαστήριο με ssh, χρειάζεται να
πληκτρολογήσετε τον κωδικό σας. Καθώς τον πληκτρολογείτε, τα bytes του
κωδικού σας ταξιδεύουν στο δίκτυο ενσύρματα ή ασύρματα (θα μάθετε
αργότερα πως) και καταλήγουν στον υπολογιστή του εργαστηρίου ώστε να
πάρετε πρόσβαση. Με παρεμφερή διαδικασία μπαίνετε στο webmail σας, το
instagram σας και ένα σωρό άλλες υπηρεσίες. Όμως … δεν μπορεί ο
οποιοσδήποτε να δει αυτά τα bytes που στέλνετε και επομένως να δει τον
κωδικό σας; Η απάντηση είναι ευτυχώς όχι και για αυτό ευχαριστούμε τον
τομέα της κρυπτογραφίας (‘Cryptography’, χ.χ.). Σε
αυτήν την άσκηση, θα ασχοληθούμε με έναν από τους πιο φημισμένους
αλγορίθμους κρυπτογραφίας, τον αλγόριθμο RSA.
Ο αλγόριθμος RSA κοινοποιήθηκε για πρώτη φορά το 1977 (‘Rivest–Shamir–Adleman (RSA)’, χ.χ.). Πήρε το όνομά του από τα επώνυμα των εφευρετών του (Rivest-Shamir-Adleman - Εικόνα 2) και η βασική ιδέα πίσω από τον αλγόριθμο είναι παρόμοια με όλα τα συστήματα κρυπτογραφίας που έχουμε σήμερα. Χρειαζόμαστε: (1) μια συνάρτηση encrypt που να “κρύβει” το μήνυμά μας ώστε να μην μπορεί κάποιος άλλος να το διαβάσει καθώς το στέλνουμε και (2) μια συνάρτηση decrypt η οποία να παίρνει το κρυπτογραφημένο μήνυμά μας και να το μετατρέπει (αποκρυπτογραφεί) στο αρχικό.

Οι εφευρέτες του RSA με φορεσιά 70s (όσο Disco-style επιτρεπόταν τότε). Εικονίζονται οι Adi Shamir (αριστερά), Ron Rivest (κέντρο), και Leonard Adleman (δεξιά) μπροστά σε πίνακα στο MIT. 30 χρόνια αργότερα όλος ο κόσμος θα χρησιμοποιεί τον αλγόριθμό τους.
Πως όμως μπορούμε να “κρύψουμε” το μήνυμά μας; Η βασική ιδέα του RSA είναι η εξής: έστω ότι το μήνυμα που θέλουμε να στείλουμε είναι ένας ακέραιος $m$. Τότε για να κρύψουμε το μήνυμά μας αρκεί να το υψώσουμε σε μια μεγάλη δύναμη: $m^x$. Η αποκρυπτογράφηση μπορεί να γίνει εξίσου απλά, αρκεί να βρούμε έναν αριθμό $y$ έτσι ώστε $\left(m^x\right)^y = m$. Βλέποντας αυτό το παράδειγμα, ίσως σκέφτεστε ότι $x = 2$ και $y = \frac{1}{2}$ είναι μια πιθανή λύση στο πρόβλημά μας. Η σκέψη σας είναι σωστή, αλλά επειδή οποιοσδήποτε μπορεί να υπολογίσει την τετραγωνική ρίζα ενός αριθμού δεν μπορούμε να χρησιμοποιήσουμε αυτές τις πράξεις και αριθμούς για ασφαλή κρυπτογράφηση. Για να δούμε ποιους αριθμούς και πράξεις μπορούμε να χρησιμοποιήσουμε, χρειαζόμαστε πρώτα κάποιους ορισμούς:
Ορισμός 3. Ένας φυσικός αριθμός p μεγαλύτερος του 1 ονομάζεται *πρώτος (prime) (‘Prime Numbers’, χ.χ.) όταν έχει σαν μόνους διαιρέτες (το υπόλοιπο της διαίρεσης είναι 0) το 1 και το p. Για παράδειγμα, το 17 είναι πρώτος αριθμός, ενώ το 42 δεν είναι, αφού έχει σαν διαιρέτες το 2, το 3 και το 7, εκτός από τους 1 και 42. Μπορείτε να επιβεβαιώσετε ότι οι πρώτοι αριθμοί που είναι μικρότεροι από το 100 είναι οι εξής:*
\(2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97\)
Μαθηματικοί στο παρελθόν έχουν ασχοληθεί με πολλά γνωστά προβλήματα όπως η κατανομή τους (‘Riemann Hypothesis’, χ.χ.). Μέχρι σήμερα, δεν έχει βρεθεί μια συνάρτηση που να παράγει τους πρώτους αριθμούς αποδοτικά (‘Formulas for Primes’, χ.χ.).
Ορισμός 4. Δύο ακέραιοι $a$ και $b$ είναι *πρώτοι μεταξύ τους ή σχετικά πρώτοι (coprime) (‘Coprimes ’, χ.χ.) όταν ο μέγιστος κοινός διαιρέτης τους είναι το 1, δηλαδή $\text{gcd}(a, b) = 1$. Για παράδειγμα, οι αριθμοί 8 και 9 είναι coprime εφόσον το $\text{gcd}(8, 9) = 1$ παρόλο που κανείς από τους δυο τους δεν είναι ο ίδιος πρώτος.*
Ορισμός 5. Η συνάρτηση $\phi : \mathbb{N} \rightarrow \mathbb{N}$ του Euler (γνωστή και ως totient function (‘Euler’s Totient Function’, χ.χ.)) δέχεται έναν φυσικό αριθμό n και επιστρέφει το πλήθος των φυσικών αριθμών που είναι μικρότεροι του n και comprime με το n. Για παράδειγμα, $\phi(9) = 6$, εφόσον υπάρχουν ακριβώς έξι coprime με το 9: 1, 2, 4, 5, 7 και 8. Η συνάρτηση $\phi$ έχει την πολλαπλασιαστική ιδιότητα, δηλαδή για κάθε δύο φυσικούς $a$, $b$ με $\text{gcd}(a, b) = 1$ ισχύει ότι $\phi(a\cdot b) = \phi(a)\cdot \phi(b)$. Επίσης, αν ο αριθμός $a$ είναι πρώτος, τότε ισχύει πως $\phi(a) = a - 1$. Για παράδειγμα: $\phi(5) = 4$, εφόσον οι αριθμοί 1, 2, 3, 4 είναι coprime ως προς το 5.
Έχοντας τους παραπάνω ορισμούς, μπορούμε επιτέλους να ορίσουμε τους περιορισμούς για να λειτουργήσει σωστά ο αλγόριθμος RSA:
-
Έστω οι ακέραιοι $e$, $d$, $p$, $q$ (το μυστικό) και ο ακέραιος $m$ (το μήνυμα)
-
Έστω ο ακέραιος $N = p \cdot q$.
-
Περιορισμός: όλοι οι ακέραιοι πρέπει να είναι θετικοί.
-
Περιορισμός: το μήνυμα $m$ πρέπει να είναι μικρότερο του $N$.
-
Περιορισμός: οι ακέραιοι $p$ και $q$ είναι πρώτοι.
-
Περιορισμός: ο ακέραιος $e$ είναι coprime με το $\phi(N)$.
-
Περιορισμός: οι ακέραιοι $e$ και $d$ είναι αντίστροφοι, δηλαδή: $e \cdot d \bmod \phi(N) = 1$.
Με βάση τους παραπάνω περιορισμούς, μπορούμε πλέον να ορίσουμε την συνάρτηση κρυπτογράφησης encrypt ως:
\[\begin{aligned} encrypt(m) & = m^e \bmod N \end{aligned}\]Αντίστοιχα αν μας δώσουν έναν ακέραιο $c$ ($=m^e \bmod N$) που είναι το κρυπτογραφημένο μήνυμα, μπορούμε να το αποκρυπτογραφήσουμε, χρησιμοποιώντας την συνάρτηση decrypt:
\[\begin{aligned} decrypt(c) & = c^d \bmod N \end{aligned}\]Το γιατί η παραπάνω πράξη μας δίνει το αρχικό μας μηνύμα είναι μεγάλη ιστορία$c^d \bmod N = \left(m^e\right)^d\bmod N = m^{e\cdot d}\bmod N = m^{1 + k\phi(N)} \bmod N = m \bmod N$αλλά μπορείτε να βρείτε όλα τα βήματα της απόδειξης στην Wikipedia (‘Euler’s Theorem’, χ.χ.).
Φτάσαμε επιτέλους στο ζητούμενο αυτής της άσκησης: να γράψετε ένα πρόγραμμα το οποίο να μπορεί να κρυπτογραφεί και να αποκρυπτογραφεί μηνύματα χρησιμοποιώντας τον παραπάνω αλγόριθμο RSA. Τα βήματα που θα υλοποιήσετε είναι αντίστοιχα με αυτά που τρέχουν κάθε φορά που κάνετε σύνδεση σε μια απομακρυσμένη υπηρεσία σήμερα στο διαδίκτυο! Οι τεχνικές προδιαγραφές ακολουθούν.
Τεχνικές Προδιαγραφές
-
Repository Name: progintro/hw1-<YourUsername>
-
C Filepath: rsa/src/rsa.c
-
Το πρόγραμμά θα πρέπει να παίρνει 5 ορίσματα από την γραμμή εντολών στην μορφή
./rsa op e d p q. Tο πρώτοopεπιτρέπεται να είναι “enc” (για encryption) και “dec” για decryption. Τα υπόλοιπα ορίσματα θα είναι ακέραιοι αριθμοί και θα είναι στο εύρος $[-10^{18}, 10^{18}]$. Αν το πρόγραμμα εκτελεστεί με ορίσματα που δεν ακολουθούν τις παραπάνω προδιαγραφές, πρέπει να εκτυπώσει αντίστοιχο μήνυμα όπως στα παρακάτω παραδείγματα και να επιστρέφει με κωδικό εξόδου (exit code) 1. -
Το πρόγραμμα θα πρέπει να διαβάζει το μήνυμα $m$ από την πρότυπη είσοδο (standard input) ως έναν δεκαδικό αριθμό επίσης στο εύρος $[-10^{18}, 10^{18}]$. Γενικά, δεν θα σας ζητηθεί να χρησιμοποιήσετε ακεραίους με περισσότερα από 64 bits.
-
Αν η είσοδος του χρήστη δεν πληροί τους περιορισμούς του αλγορίθμου RSA το πρόγραμμά σας πρέπει να τερματίζει με κωδικό εξόδου 1 και αντίστοιχο μήνυμα λάθους όπως δείχνουμε παρακάτω στις ενδεικτικές εκτελέσεις.
-
Το αρχείο C που θα υποβληθεί πρέπει να μεταγλωττίζεται χωρίς ειδοποιήσεις για λάθη και με κωδικό επιστροφής (exit code) που να είναι 0. Συγκεκριμένα, το αρχείο σας πρέπει να μπορεί να μεταγλωττιστεί επιτυχώς με την ακόλουθη εντολή σε ένα από τα μηχανήματα του εργαστηρίου (linuxXY.di.uoa.gr):
gcc -O3 -Wall -Wextra -Werror -pedantic -o rsa rsa.c -
README Filepath: rsa/README.md
-
Πρέπει να ολοκληρώνει την εκτέλεση μέσα σε: 1 δευτερόλεπτο.
Παρακάτω παραθέτουμε αλληλεπιδράσεις με μια ενδεικτική λύση. Ας δοκιμάσουμε να στείλουμε το μήνυμα “42” ($m = 42$) χρησιμοποιώντας το μυστικό “257 257 173 193” ($e = 257$, $d = 257$, $p = 173$, $q = 193$):
$ echo 42 | ./rsa enc 257 257 173 193
6990
$ echo $?
0
Άρα το κρυπτογραφημένο μήνυμα που μπορούμε να στείλουμε είναι ο αριθμός $c = 6990$. Είναι σωστός; Πρέπει να κάνουμε την πράξη $42^{257}\bmod (173 \cdot 193)$ το οποίο όντως αν χρησιμοποιήσουμε ένα online calculator (‘Online RSA Calculator’, χ.χ.) φαίνεται σωστό (αντίστοιχα μπορείτε να κάνετε πειράματα με τους δικούς σας συνδυασμούς αριθμών). Για να δούμε αν μπορούμε να αποκρυπτογραφήσουμε το αρχικό μας μήνυμα:
$ echo 6990 | ./rsa dec 257 257 173 193
42
$ echo $?
0
Πήραμε όντως πίσω το αρχικό μας μήνυμα! Παρακάτω δοκιμάζουμε να κρυπτογραφήσουμε και να αποκρυπτογραφήσουμε διάφορους συνδυασμούς που καλύπτουν τις προδιαγραφές παραπάνω:
$ ./rsa
Usage: ./rsa enc|dec <exp_exp> <priv_exp> <prime1> <prime2>
$ echo $?
1
$ ./rsa pop 1 2 3 4
First argument must be 'enc' or 'dec'
$ echo $?
1
$ ./rsa enc 1 2 -3 4
Negative numbers are not allowed
$ echo $?
1
$ ./rsa enc 1 2 3 4
p and q must be prime
$ echo $?
1
$ ./rsa enc 3 6 17 19
e is not coprime with phi(N)
$ echo $?
1
$ ./rsa enc 5 6 17 19
e * d mod phi(N) is not 1
$ echo $?
1
$ echo 500 | ./rsa enc 5 173 17 19
Message is larger than N
$ echo $?
1
$ echo -42 | ./rsa enc 5 173 17 19
Negative numbers are not allowed
$ echo $?
1
$ echo 42 | ./rsa enc 5 173 17 19
264
$ echo 42 | ./rsa enc 17 26153 131 229
27187
$ echo 27187 | ./rsa dec 257 257 173 193
5343
$ echo 27187 | ./rsa dec 17 26153 131 229
42
$ echo 117 | ./rsa enc 17 26153 131 229 | ./rsa dec 17 26153 131 229
117
$ echo 43434343 | ./rsa enc 65537 2278459553 62971 38609 |
./rsa dec 65537 2278459553 62971 38609
43434343
$ echo 42 | ./rsa enc 65537 2278459553 62971 38609 > enc_msg
$ cat enc_msg
741088023
$ time ./rsa dec 65537 2278459553 62971 38609 < enc_msg
42
real 0m0.011s
user 0m0.004s
sys 0m0.008s
Καθώς οι εκθέτες του μυστικού στον οποίο υψώνουμε το μήνυμα γίνονται μεγαλύτεροι, είναι πιθανό πως το πρόγραμμά σας θα αρχίσει να παίρνει όλο και περισσότερο χρόνο για να τερματίσει. Αν παρατηρήσετε πως κάτι τέτοιο συμβαίνει και στον δικό σας αλγόριθμο, μπορείτε να δοκιμάσετε βελτιωμένους αλγόριθμους υπολογισμού της δύναμης ενός ακεραίου (‘Repeated Squaring’, χ.χ.; ‘Modular Exponentiation’, χ.χ.).
Στο αρχείο README.md πρέπει να προσθέσετε οποιεσδήποτε παρατηρήσεις σας κατά την διεκπεραίωση της άσκησης. Ο κώδικας απαιτείται να είναι καλά τεκμηριωμένος με σχόλια καθώς αυτό θα είναι μέρος της βαθμολόγησης.
Παραγοντοποίηση (factor - Bonus 50 Μονάδες)
Αυτή η άσκηση είναι Bonus, δηλαδή η λύση της δεν είναι απαραίτητη για να πάρει κάποιος/α όλες τις μονάδες της Εργασίας 1. Οι μονάδες από την όποια υποβολή για αυτήν την άσκηση θα προστεθούν στον τελικό σας βαθμό του μαθήματος που περιλαμβάνει τις ασκήσεις. Σε αυτήν την άσκηση, θα ασχοληθούμε (και πάλι!) με ένα πρόβλημα που είχαμε δει στο Δημοτικό, το πρόβλημα της παραγοντοποίησης!
Μάθαμε στα διακριτά μαθηματικά πρόσφατα, ότι κάθε μη πρώτος (σύνθετος/composite) αριθμός, μπορεί να γραφτεί σαν γινόμενο δύο ή περισσότερων πρώτων αριθμών. Επομένως η παραγοντοποίηση (factorization) (‘Factorization’, χ.χ.) ενός φυσικού αριθμού n είναι το πρόβλημα της εύρεσης των πρώτων παραγόντων που το γινόμενό τους μας δίνει το n. Για παράδειγμα, η παραγοντοποίηση του αριθμού $42$ είναι $2\cdot 3 \cdot 7$. Συγκεκριμένα, σε αυτήν την άσκηση θα ασχοληθούμε με την παραγοντοποίηση μιας συγκεκριμένης κατηγορίας σύνθετων αριθμών, τους ημιπρώτους (semiprimes).
Ορισμός 6. Ένας φυσικός αριθμός λέγεται ημιπρώτος (semiprime) (‘Semiprime Numbers’, χ.χ.), όταν είναι το γινόμενο ακριβώς δύο πρώτων αριθμών. Για παράδειγμα, ο αριθμός $46$ είναι semiprime ($2\cdot 23$) όπως και ο αριθμός $9$ ($3\cdot 3$). Αντίθετα, ο αριθμός $42$ δεν είναι semiprime.
Το πρόβλημα της παραγοντοποίησης ημιπρώτων φαίνεται απλό: το μόνο που πρέπει να κάνουμε είναι να βρούμε δύο αριθμούς που το γινόμενό τους να μας δίνει τον αριθμό με τον οποίο ξεκινήσαμε. Παρόλα αυτά, κανένας/καμία δεν έχει βρειμέχρι στιγμής!μια αποδοτική λύση σε αυτό το πρόβλημα (‘Integer Factorization Records’, χ.χ.) παρόλα τα χρηματικά έπαθλα που έχουν ανακυρηχθεί (‘The RSA 2048 Challenge’, χ.χ.; ‘The RSA129 Challenge’, χ.χ.). Από την μία, αυτό είναι καλό, η ασφάλεια της κρυπτογράφησης που είδαμε στον αλγόριθμο RSA παραπάνω στηρίζεται στο ότι η παραγοντοποίηση μεγάλων αριθμών είναι ένα δύσκολο πρόβλημα και επομένως μπορούμε να συνεχίσουμε να χρησιμοποιούμε αυτόν τον αλγόριθμο για να μπαίνουμε στα αγαπημένα μας site. Από την άλλη, συνεχίζουμε και ψάχνουμε για πιο γρήγορες λύσεις, μιας και υποψιαζόμαστε ότι είναι πολύ πιθανό ένας γρήγορος αλγόριθμος να υπάρχει και απλά να μην έχουμε βρει ακόμα!
Σε αυτήν την άσκηση λοιπόν, καλείστε να γράψετε ένα αποδοτικό πρόγραμμα το οποίο να παραγοντοποιεί ημιπρώτους (semiprimes). Ακολουθούν οι τεχνικές προδιαγραφές.
Τεχνικές Προδιαγραφές
-
Repository Name: progintro/hw1-<YourUsername>
-
C Filepath: factor/src/factor.c
-
Το πρόγραμμά θα πρέπει να παίρνει ένα όρισμα από την γραμμή εντολών στην μορφή
./factor semiprime, με το πρώτο (semiprime) να είναι ο ημιπρώτος που θέλουμε να παραγοντοποιήσουμε. Αν το πρόγραμμα εκτελεστεί με ορίσματα που δεν ακολουθούν τις παραπάνω προδιαγραφές, πρέπει να εκτυπώσει αντίστοιχο μήνυμα όπως στα παρακάτω παραδείγματα και να επιστρέφει με κωδικό εξόδου (exit code) 1. -
Όλοι οι δεκαδικοί ακέραιοι που θα δοθούν στο πρόγραμμά σας θα είναι ημιπρώτοι και στο εύρος: $[0, 2^{127}]$. Για οποιαδήποτε άλλη είσοδο, το πρόγραμμά σας πρέπει να τερματίζει με κωδικό εξόδου 1.
-
Το αρχείο C που θα υποβληθεί πρέπει να μεταγλωττίζεται χωρίς ειδοποιήσεις για λάθη και με κωδικό επιστροφής (exit code) που να είναι 0. Συγκεκριμένα, το αρχείο σας πρέπει να μπορεί να μεταγλωττιστεί επιτυχώς με την ακόλουθη εντολή σε ένα από τα μηχανήματα του εργαστηρίου (linuxXY.di.uoa.gr):
gcc -O3 -Wall -Wextra -Werror -o factor factor.c -lm -
Μορφοποίηση: το αρχείο που θα υποβληθεί πρέπει να έχει μορφοποίηση σύμφωνη με το C/C++ στυλ της Google. Για να μορφοποιήσετε το αρχείο σας, μπορείτε να τρέξετε την ακόλουθη εντολή:
clang-format -i -style=Google factor.cσε έναν υπολογιστή εργαστηρίου. Μη μορφοποιημένα προγράμματα δεν θα εξεταστούν. -
README Filepath: factor/README.md
-
Ένα αρχείο που να περιέχει ένα στοιχείο εισόδου και ένα εξόδου *διαφορετικά* από αυτά της εκφώνησης. Συγκεκριμένα προτείνουμε να βάλετε έναν συνδυασμό που θεωρείται ότι είναι δύσκολος να γίνει σωστός κατά την υλοποίηση.
-
input Filepath:
factor/test/input.txt -
output Filepath:
factor/test/output.txt
Για παράδειγμα, το περιεχόμενο του input.txt αρχείου μπορεί να είναι: “
93” και του αντίστοιχου output.txt: “3 31”. Προσοχή: αυτό το παράδειγμα δεν θα γίνει δεκτό από την άσκηση επειδή αυτό το input-output ζευγάρι υπάρχει ήδη παρακάτω, επομένως πρέπει να διαλέξετε κάποιο άλλο. -
-
Πρέπει να ολοκληρώνει την εκτέλεση μέσα σε: 10 δευτερόλεπτα.
-
Δεν επιτρέπεται χρήση προϋπολογισμένων αποτελεσμάτων. Το πρόγραμμά σας πρέπει να υπολογίζει το αποτέλεσμα χωρίς “πρότερη γνώση”, δηλαδή χωρίς να έχετε ήδη κωδικοποιήσει παραγοντοποιήσεις ημιπρώτων που έχετε βρει από προηγούμενους υπολογισμούς σας μέσα στον κώδικα.
-
Καθώς αυτή η εργασία είναι Bonus, θα ελέγξουμε και ποιοτικά χαρακτηριστικά της υποβολής. Μια ιδιαίτερα δυσνόητη ή μη διαχειρίσιμη λύση (π.χ., 6 nested if-else, 35 μεταβλητές στην ίδια συνάρτηση κτλ) θα οδηγήσει σε αφαίρεση μονάδων κατά την κρίση του εξεταστή.
Παρακάτω παραθέτουμε την αλληλεπίδραση με μια ενδεικτική λύση:
$ ./factor
Usage: ./factor <semiprime>
$ echo $?
1
$ ./factor 93
Factors: 3 31
$ echo $?
0
$ ./factor 9827348119
Factors: 613 16031563
$ # level: very hard
$ ./factor 2524891914334062643
Factors: 1175747593 2147477851
$ # level: extremely hard
$ ./factor 809724910412139638697047
Factors: 783108713587 1033987869581
$ # level: this is impossible
$ ./factor 66162145239900452012870189875803961
Factors: 206547667773749927 320323855277677343
Στο αρχείο README.md πρέπει να προσθέσετε οποιεσδήποτε παρατηρήσεις κάνατε κατά την διεκπεραίωση της άσκησης. Ο κώδικας απαιτείται να είναι καλά τεκμηριωμένος με σχόλια καθώς αυτό θα είναι μέρος της βαθμολόγησης. Οι 10 γρηγορότερες λύσεις θα μοιραστούν ένα bonus (extra) 500 μονάδων κατανεμημένων αναλογικά με τον παράγοντα $\frac{1}{T}$ (μέχρι το max: 200 μονάδες ανά υποβολή), όπου $T$ είναι ο συνολικός χρόνος που απαιτεί ο αλγόριθμος της υλοποίησης για να παραγοντοποιήσει όλους τους ακεραίους που του δόθηκαν. Αν δούμε μια ιδιαίτερα ενδιαφέρουσα/αποδοτική λύση, θα ζητήσουμε μια παρουσίαση από το παιδί που την υλοποίησε.
‘Alexandria’. χ.χ. https://en.wikipedia.org/wiki/Alexandria.
‘Algorithm comes from Al-Khwarizmi’. χ.χ. https://en.wikipedia.org/wiki/Al-Khwarizmi.
‘Coprimes ’. χ.χ. https://en.wikipedia.org/wiki/Coprime_integers.
‘Cryptography’. χ.χ. https://en.wikipedia.org/wiki/Cryptography.
‘Euclid’. χ.χ. https://en.wikipedia.org/wiki/Euclid.
‘Euclid Algorithm Visualization’. χ.χ. https://www.geogebra.org/m/ztbesvsd.
‘Euclid’s Elements’. χ.χ. https://en.wikipedia.org/wiki/Euclid%27s_Elements.
‘Euclidean Algorithm’. χ.χ. https://en.wikipedia.org/wiki/Euclidean_algorithm.
‘Euler’s Theorem’. χ.χ. https://en.wikipedia.org/wiki/Euler%27s_theorem.
‘Euler’s Totient Function’. χ.χ. https://en.wikipedia.org/wiki/Euler%27s_totient_function.
‘Factorization’. χ.χ. https://en.wikipedia.org/wiki/Factorization.
‘Formulas for Primes’. χ.χ. https://en.wikipedia.org/wiki/Formula_for_primes.
‘Integer Factorization Records’. χ.χ. https://en.wikipedia.org/wiki/Integer_factorization_records.
‘Library of Alexandria’. χ.χ. https://en.wikipedia.org/wiki/Library_of_Alexandria.
‘Modular Exponentiation’. χ.χ. https://en.wikipedia.org/wiki/Modular_exponentiation.
‘Online RSA Calculator’. χ.χ. https://rsa-calculator.netlify.app/.
Pollard, Justin, και Howard Reid. 2006. The Rise and Fall of Alexandria: Birthplace of the Modern Mind. Viking Adult.
‘Prime Numbers’. χ.χ. https://en.wikipedia.org/wiki/Prime_number.
‘Repeated Squaring’. χ.χ. https://en.wikipedia.org/wiki/Exponentiation_by_squaring.
‘Riemann Hypothesis’. χ.χ. https://en.wikipedia.org/wiki/Riemann_hypothesis.
‘Rivest–Shamir–Adleman (RSA)’. χ.χ. https://en.wikipedia.org/wiki/RSA_(cryptosystem).
‘Semiprime Numbers’. χ.χ. https://en.wikipedia.org/wiki/Semiprime.
‘The RSA 2048 Challenge’. χ.χ. https://en.wikipedia.org/wiki/RSA_numbers#RSA-2048.
‘The RSA129 Challenge’. χ.χ. https://www.youtube.com/watch?v=YQw124CtvO0.
‘Οργανισμός για το μάθημα (GitHub progintro) ’. χ.χ. https://github.com/progintro.
‘Πρόσκληση για Εργασία 1 ’. χ.χ. https://classroom.github.com/a/Fi7KL10s.
-
Να αναφέρουμε ότι ο αυθεντικός αλγόριθμος του Ευκλείδη ήταν διαφορετικός (‘Euclidean Algorithm’, χ.χ.), εδώ χρησιμοποιούμε μια πιο μοντέρνα εκδοχή του. ↩